Анализ сетей

Графы это математическая формализация сетей. Поскольку я до дипломной работы перерыл много материалов, то тут буду собирать интересные доклады по этой общей теме. Эта статья составлена на основе курсов лекций Networked Life (Michael Kearns, Pennsylvania) и Social Network Analysis (Lada Adamic, Michigan) в Coursera.

Интереснейшие проблемы анализа сетей это поиск кратчайшего пути, визуализация и заражение

Терминология

Наука изучения сетей междисциплинарная, поэтому и термины могут применяться разные.

Точки	Линии	Область применения
Vertices (вершины)	Edges, arcs (рёбра)	Математика
Nodes (узлы)	Links (связи)	Инфотехнологии
Sites	Bonds	Физика
Actors	Ties, relations	Социология

Программные инструменты 

Gephi, Netlogo, iGraph, Pajek, UCINet, NodeXL, NetworkX, SoNIA.

Компоненты

В зависимости от того, как моделируется сеть (направленно или нет), зависят и некоторые её характеристики. Можно говорить о сильно связанном компоненте направленной сети, если из каждой его вершины можно попасть в любую другую. Большие естественные сети рано или поздно образуют гигантский компонент

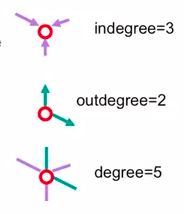
Особенности естественных сетей

Кратчайший путь определяется только если сеть не имеет изолированных узлов (disconnected component). Проблема выражается в ограниченности видимости конкретного узла. Так, в социальных сетях человек ограничен знанием о своём окружении, поэтому он не видит всей картины, связывающей его с произвольным узлом остальной сети (small world effect).

Поиск пути в социальных сетях решается географическими и родственными связями (убывают по мере распространения), а дальше профессиональными и образовательными связями (увеличиваются по мере распространения).

Естественные сети (в отличие от скажем случайных сетей),  стремятся к минимизации кратчайшего пути и по мере роста числа узлов, среднее кратчайшее расстояние (диаметра сети) асимптотически уменьшается. Социальные сети на основе эмпирических исследований Траверса и Милграма (1969 г.), Лешковеца и Горвица (2008 г.) и Бэкстрома и др. (2012 г.) показывает что значение диаметра в районе 5.

Второе особенное свойство естественных сетей - высокая степень скоплений. Вершины часто предпочитают образовывать локальные группы с повышенным числом связей между собой.

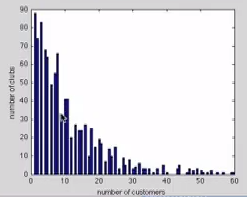
Наконец третье свойство - длинный хвост в распределении степеней вершин (heavy tailed degree distribution, степенной закон, принцип Парето 20/80). Это проявляется в том, что в обществе есть редкие вершины, число связей у которых очень велико, а в среднем по сети "популярность" падает довольно резко и нелинейно

Заражение (перколяция, диффузия) в сетях может происходить необычайно быстро из-за пограничного свойства как структуры сети, так и свойств заражения (tipping point, threshold). Если взять случайно сгенерированный граф у которого средняя степень узла равна 4, то легко увидеть что при 100% степени заражения, порядка 90% узлов будет покрыто.

\[e=d*N/2\]

e - число рёбер
d - средняя степень узла
N - число узлов в сети

Число рёбер для ненаправленного графа

Аналогично, можно усложнять модель заражения, учитывать процент диффузии и регенерации, например для моделирования лесных пожаров с эволюционной точки зрения

Скопления

Для любой вершины можно определить степень скопления (clustering coefficient) как показатель взаимосвязанности её соседей. Если все вершины связаны, то такой подграф называется клик (clique) и имеет коэффицент 1. Теперь для расчёта коэффициента среднего скопления, достаточно просчитать коэффициент для всех вершин и взять среднее значение

\[C(u) = \frac{k+m}{k(k-1) /2 }\]

C(u) - коэффициент кластеризации вершины u
k - степень вершины
m - число связей "между друзьями"

Коэффициент кластеризации вершины

Коэффициент кластеризации имеет смысл сравнивать не просто с нулём, а со средней плотностью рёбер в графе, которая одновременно является и вероятностью что две вершины имеют общую связь

\[p = \frac{E}{N(N-1)/2}\]

p - плотность рёбер в графе
E - число рёбер в графе
N - число вершин

Плотность рёбер

Для естественных сетей C(u) значительно больше p

Моделирование скоплений

В случайных графах связи между вершинами распределены равномерно. В социальных сетях, новые связи возникают по принципу "друг моего друга - мой друг", при этом вероятность возникновения новой связи может расти в зависимости от числа общих друзей не линейно:

\[y \sim p + (\frac{x}{N})^a\]

y - вероятность создания новой связи между двумя вершинами
p - вероятность случайной связи
x - число общих друзей между вершинами
N - размер всей сети

alpha-модель

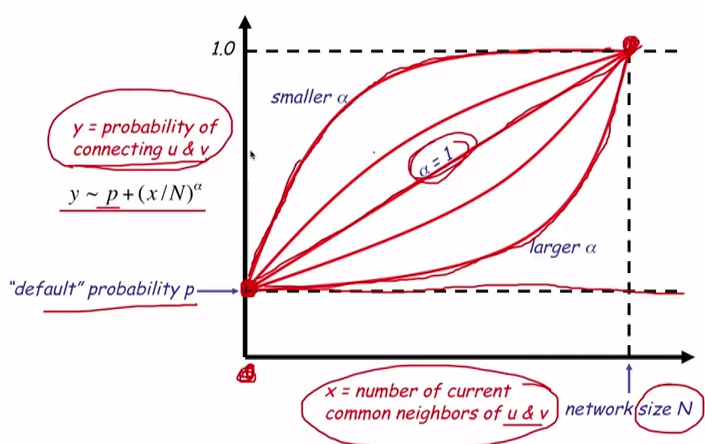
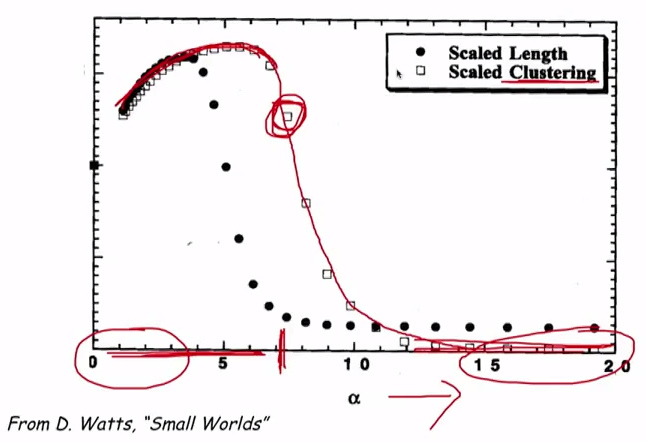
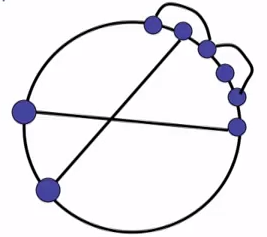
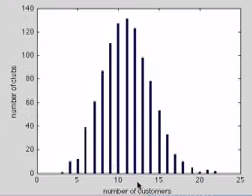
Если теперь сгенерировать много случайных графов при разных значениях степени альфа, то можно заметить что коэффициент скоплений в сетях падает, по мере роста степени (и соответсвенно уменьшении зависимости от друзей) и приближения модели к случайным связям. Вторая модель не столько учитывает формирование сети на основе друзей, сколько на основе физического положения.

Предпочтительное связывание

Описанные модели формирование скоплений тем не менее не объясняют почему распределение степеней вершин подчиняется степенному закону. 

\[p(k) = Сk^{-\alpha}\]

p(k) - вероятность вершины иметь степень k
α, C - константы

Распределение со степенным законом

Предпочтительное связывание (preferrential attachment, cumulative advantage) объясняет неравенства возникающие в сетях, в том числе почему богатые становятся богаче, почему у поп-звёзд так много поклонников. В целом это сводится к тому, что чем больше у вершины есть ресурсов, тем легче ей получить ещё - через дополнительную рекомендацию друзей, предубеждение, славу и тп.

Навигация

Для понимания естественных сетей, стоит поговорить о процессах навигации и распространении сигналов. Они должы учитывать как структурные особенности сети, так и алгоритм выбора оптимального пути.

Модель Клейнберга предполагает что сеть упорядочена в матрицу k на k и каждая вершина знает свои координаты. Передача сообщения в таком случае сводится к выбору соседней вершины, наиболее близкой географически к глобальной цели. При этом можно ввести сопротивление в движении 

\[p(d) \propto (1/d)^r\]

p - вероятность новой связи между двумя вершинами
d - расстояние между вершинами
r>=0 - степень, влияющая на поведение

При очень больших r, передача сообщений происходит только локально и кратчайшие расстояния до дальних вершин могут даже не существовать.

Приуменьшении r, падает сопротивление от расстояния, но увеличивается алгоритмическая сложность поиска кратчайшего расстояния

Важные вершины

До этого всё что касалось характеристик, описывало всю сеть целиком, но единичные вершины также критично важны.

Pagerank

Один из способов оценки важности вершин в направленном графе основывается на пошаговом рекурсивном алгоритме вычисления важности вершины основываясь на важности ссылающихся на эту вершину входящих рёбрах-ссылках (out-degree). В случае если эти величины у всех вершин остаются неизменными и граф не меняется, то можно считать что сеть достигла равновесия.

\[R(p) = \sum_{q \in POINTS(p)} \frac {R(q)}{out(q)}\]

R(p) - pagerank вершины p
R(q) - pagerank вершины q которая ссылается на p (принадлежит множеству POINTS)
out(q) - число исходящих ссылок из q

page rank

Вот например как выглядит расчёт для некоторых вершин..

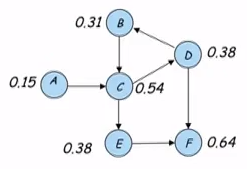
Рациональные процессы в сетях

Модель сегрегации Шеллинга

Шеллинг показал, что если вершины могут выступать как люди и изменять своё местоположение в матричной сети, переезжая в ближаюшую не занятую ячейку, то при случайном начальном расположении и при требовании вершины к своим соседям в 40% похожести, возникают сегрегированные области, подобно гетто-районам расовой сегрегации.

См. эмулятор.

Начальное случайное положение

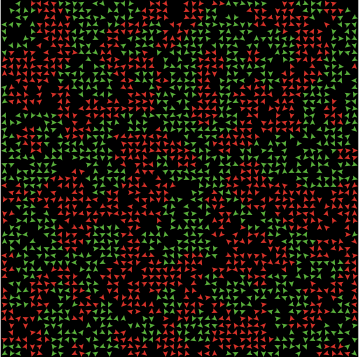Сегрегация при 40 процентах требований достигает 80 процентов похожести